|
 Broadening the knowledge base: Nozzle performance data Broadening the knowledge base: Nozzle performance data
Nozzle performance is evaluated by examining data such as pressure/flow rate, pressure/spray angle, flow distribution, spray impact distribution, droplet size, etc. But nozzle manufacturers have not always tested the performance of their products in every conceivable situation. Consequently, even manufacturers who possess the necessary measurement devices may not always have on hand the entire (and vast) spectrum of data that pertains their standard range of spray nozzles. The reason for this is that major manufacturers' printed product catalogs typically contain several tens of thousands of standard spray nozzles, so an enormous amount of time and money would be required to obtain complete data on every product. Furthermore, it is conceivable that obtaining data for each spray nozzle would increase the cost of the spray nozzle itself. Almost all nozzle manufacturers do posses measurement devices for their own research and development. A customer may be charged by a manufacturer for carrying out tests at the user's request.
Pressure/flow-rate characteristics data |
Pressure/spray-angle characteristics data
|
Flow distribution data |
Spray impact distribution data | Droplet size data
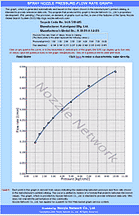
 Pressure/Flow-rate characteristics data Pressure/Flow-rate characteristics dataIn almost all cases, nozzle flow rate varies according to inlet pressure. In manufacturers' product catalogs, pressure values (typically contrasted with flow rate values) are listed for each model. A formula (provided in the manufacturer's product catalog) can be used to determine the flow rate value at pressures not shown in the catalog, or the manufacturer's advice can be sought. (For nozzles that spray liquids, the SGS will, on demand, generate a graph that represents the relationship between pressure and flow rate. This simplifies the task of obtaining pressure values that are not given in catalogs.)
|
 Pressure/spray-angle characteristics data Pressure/spray-angle characteristics dataIn almost all cases, spray angle varies according to inlet pressure. In manufacturers' product catalogs, pressure values (typically contrasted with spray angle values) are listed for each model. To determine a spray angle value at a pressure not given in a catalog, the manufacturer's advice should be sought.
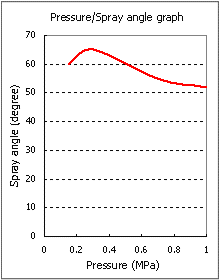 An example of a Pressure/spray angle graph
An example of a Pressure/spray angle graph
|
  Flow distribution data
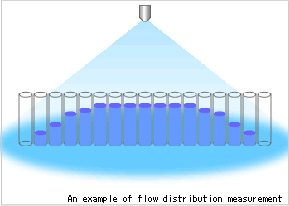 Flow distribution refers to the density of flow of the scattered droplets at a given spray distance, measured along a cross-section of the spray pattern. Nozzle manufacturers have devised their own methods to measure flow distribution. One such method is to arrange containers on a level surface (as the illustration on the right indicates) and to measure the water level in each after spraying for a certain period of time. Flow distribution refers to the density of flow of the scattered droplets at a given spray distance, measured along a cross-section of the spray pattern. Nozzle manufacturers have devised their own methods to measure flow distribution. One such method is to arrange containers on a level surface (as the illustration on the right indicates) and to measure the water level in each after spraying for a certain period of time.
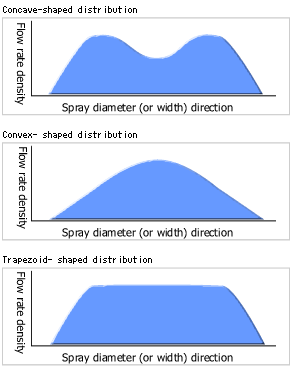 Flow distribution is classified into three types, concave, convex, and trapezoid, with the type of flow distribution varying according to the type of spray nozzle. Moreover, flow distribution readings vary from manufacturer to manufacturer (even if the spray nozzles in question actually produce the same spray pattern). Normally, nozzle manufacturers standardize the flow distribution characteristics of their products according to nozzle type, but they may accept an order for a custom-made spray nozzle whose flow distribution is a tailored to satisfy a customer's requirements. Flow distribution is classified into three types, concave, convex, and trapezoid, with the type of flow distribution varying according to the type of spray nozzle. Moreover, flow distribution readings vary from manufacturer to manufacturer (even if the spray nozzles in question actually produce the same spray pattern). Normally, nozzle manufacturers standardize the flow distribution characteristics of their products according to nozzle type, but they may accept an order for a custom-made spray nozzle whose flow distribution is a tailored to satisfy a customer's requirements.
 Spray impact distribution data
Spray impact distribution refers to the distribution of the force of the spray as it comes into contact with the target. Each nozzle manufacturer contrives their own measurement device for this data, but there are only a small number of manufacturers in the world who possess such measurement devices. Fundamentally, pressure is proportional to spray impact in a given nozzle. When different spray nozzles deliver the same flow rate, spray impact is proportional to the square root of pressure (i.e. the velocity of the flow). The theoretical formula being as follows:
As the relationship between spray impact and flow rate is proportional, spray impact distribution is similar in shape to flow distribution (for the same spray nozzle).Spray impact and distribution vary according to a type of spray nozzle and manufacturer. Like flow distribution, spray impact distribution is also generally classified into three types (concave, convex, and trapezoid).
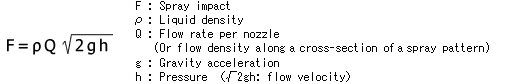
The formula above may vary according to the type of spray nozzle or pressure. Consequently, it will be necessary to factor-in a correction coefficient. The correction coefficient, however, also varies according to nozzle type or pressure. Therefore, in almost cases, spray impact is determined by means of actual measurement.
 Droplet size data
Droplet size refers to the mean diameter of liquid droplets or drop size distribution. This data is essential not only for manufacturers and scientists, but also for engineers working at enterprises concerned with the evaluation of experimental results relating to spray nozzles. (ILASS Japan)
Measurement methods for ascertaining droplet diameter
| (1) Measurement by laser beam |
|
| |
This method to uses a laser beam to measure falling droplets while they are in the atmosphere. As the droplets are not touched, this method is extremely accurate. Several thousands of droplets can be measured in an instant, and various kinds of mean diameters and distribution data are obtainable.
|
| (2) Measurement by CCD camera and stroboscope |
|
| |
A high-performance strobe is directed at the stream of falling droplets and a CCD camera, positioned opposite the strobe on the other side of the spray, captures the scene. The droplets (which are not touched and which appear stationary as a result of the flashing strobe) are displayed on a monitor where mean diameter and distribution can be measured by means of image analysis.
|
| (3) Photographic measurement by microscope |
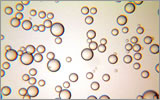 |
| |
Droplets are captured on a surface coated with silicone oil and photographed under a microscope. This is a relatively simple method of measurement. Mean diameters of droplets and their distribution is measured by ruler. |
When smaller droplets are required
The size of droplets sprayed from a spray nozzle varies according to the following factors.
| (1) Types of nozzles: |
At the same inlet pressure and flow rate, full cone type nozzles produce smaller droplets than flat spray types. The diameter of droplets produced by the former can sometimes be several times smaller than those produced by the latter. |
| (2) Pressure: |
The more inlet pressure increases, the smaller droplets become. For example, a spray nozzle that produces droplets of 1,000 microns at 1Mpa will produce much smaller droplets (of several tens of microns) if pressure is increased to 10MPa. |
| (3) Flow rate: |
The more flow rate is reduced, the smaller droplets become. For example, a spray nozzle that delivers very small volume of liquid, such as 10ml/min, produces droplets of several tens of microns. A spray nozzle that delivers high volumes of liquid, such as 1,000 l/min, produces (at the same pressure) droplets of several thousands of microns. Droplet diameter can, therefore, be several hundred times greater/smaller when flow rate is increased/decreased. |
| (4) Fluid: |
A nozzle that sprays two mixed fluids (including gas) can produce far finer droplets than a nozzle that sprays only liquid. Furthermore, if the gas flow rate of the former spray nozzle is increased, droplet size can be reduced. The mean droplet diameter of normal nozzles that spray two mixed fluids is several tens of microns. |
How to calculate the mean diameter of droplets
There are several methods to calculate the mean diameter of droplets, such as arithmetic mean diameter and Sauter mean diameter. They are distinguished according to the applications to which they are applied. In the spray nozzle field, Sauter mean diameter is used in almost exclusively, and is expressed by the following formula: Σdi³ • ni / Σdi² • ni
(The ratio of the sum total of volume to that of surface area of the measured droplets).
Therefore, the Sauter mean diameter is called "volume-surface mean diameter", and is commonly abbreviated as "D32" or "SMD".
Drop size distribution
Some applications to which spray nozzles are put require that evenly sized droplets be sprayed. Almost all spray nozzles, however, produce droplets of widely varying sizes. Including a few unusually large droplets with the thousands of regular sized droplets would have a drastic effect on calculating the mean diameter if the Sauter mean diameter formula were to be applied. Therefore, spray nozzles that produce fewer droplets nearest in size to that of the biggest droplet (i.e. droplets of a smaller mean diameter) can be identified by utilizing drop size distribution data.
 (Reference graph for drop size distribution) (Reference graph for drop size distribution)
|


 (Reference graph for drop size distribution)
(Reference graph for drop size distribution)

 Flow distribution refers to the density of flow of the scattered droplets at a given spray distance, measured along a cross-section of the spray pattern. Nozzle manufacturers have devised their own methods to measure flow distribution. One such method is to arrange containers on a level surface (as the illustration on the right indicates) and to measure the water level in each after spraying for a certain period of time.
Flow distribution refers to the density of flow of the scattered droplets at a given spray distance, measured along a cross-section of the spray pattern. Nozzle manufacturers have devised their own methods to measure flow distribution. One such method is to arrange containers on a level surface (as the illustration on the right indicates) and to measure the water level in each after spraying for a certain period of time. Flow distribution is classified into three types, concave, convex, and trapezoid, with the type of flow distribution varying according to the type of spray nozzle. Moreover, flow distribution readings vary from manufacturer to manufacturer (even if the spray nozzles in question actually produce the same spray pattern). Normally, nozzle manufacturers standardize the flow distribution characteristics of their products according to nozzle type, but they may accept an order for a custom-made spray nozzle whose flow distribution is a tailored to satisfy a customer's requirements.
Flow distribution is classified into three types, concave, convex, and trapezoid, with the type of flow distribution varying according to the type of spray nozzle. Moreover, flow distribution readings vary from manufacturer to manufacturer (even if the spray nozzles in question actually produce the same spray pattern). Normally, nozzle manufacturers standardize the flow distribution characteristics of their products according to nozzle type, but they may accept an order for a custom-made spray nozzle whose flow distribution is a tailored to satisfy a customer's requirements.